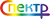ППД гамма спектрометрияПроблемы, которые приходится решать при обработке гамма спектров идентичны и для плохо разрешённых (сцинтилляционных) и для хорошо разрешённых (ППД ) спектров. Все проблемы необходимо учитывать при любых методах обработки спектров. Рассмотрим коротко основные методы обработки гамма спектров на примере обработки хорошо разрешённых спектров (ППД - охлаждаемые детекторы из особо чистого германия, германо-литиевые и кремниевые детекторы). Методы обработки гамма спектров
1. Разложение спектра на компоненты включающие и спектр непрерывного рассеяния. Рис. 1. Разложение спектра на компоненты включающие и спектр непрерывного рассеяния.
Метод позволяющий получать наиболее эффективные оценки. Основной метод обработки сцинтилляционных спектров. Но при этом подходе теряется большинство преимуществ высокого разрешения спектрометра. Все компоненты будут коррелированы из-за спектра комптоновского рассеяния и требуют, соответственно, присутствия в модели полных спектров всех нуклидов присутствующих в пробе. Расчёт точных полных спектров по таблице линий и калибровкам спектрометра практически невозможен (очень трудно точно рассчитать спектр комптоновского рассеяния гамма квантов и тормозного рентгеновского бета частиц). Калибровка спектрометра и расчёт поглощения гамма квантов в счётном образце, контейнере и среде между детектором и счётным образцом становится очень сложной задачей. В ППД гамма спектрометрии метод хорош для идентичных измерений с постоянным нуклидным составом пробы, прежде всего для ежедневной поверки спектрометра.
2. Поиск пиков и разложение спектра на спектры пиков нуклидов.
 Рис.2. Поиск пиков и разложение спектра на спектры пиков нуклидов.
До последнего времени - основной метод обработки хорошо разрешённых гамма спектров. Хорошее разрешение детектора позволяет отделить спектр пиков от спектра непрерывного рассеяния, что даёт массу преимуществ: спектры пиков нуклидов легко рассчитываются по таблицам нуклидов и калибровкам спектрометра, без проблем рассчитывается поглощение гамма квантов в зависимости от плотности и химического состава пробы, становится доступным расчёт эффективности регистрации для объёмных геометрий по эффективности регистрации для точечной геометрии, точнее рассчитываются эффекты истинных совпадений гамма квантов. Кроме того, в пакете "СПЕКТР" ("СПЕКТРРАД") оператор имеет возможность в библиотеке нуклидов указать линии, которые будут использоваться при оценках активностей нуклидов и в результате весь спектр делится на окна принимающие участие в оценивании (выделены зелёным цветом) и не принимающие участия (выделены серым цветом).
3. Разложение спектра на спектры пиков нуклидов и аппроксимация спектра непрерывного рассеяния.
 Рис. 3. Разложение спектра на спектры пиков нуклидов и аппроксимация спектра непрерывного рассеяния сплайном.
Метод хорош тем, что мы не ищем пики в спектре и соответственно застрахованы от всех погрешностей связанных с процедурой поиска пиков (не пропустим пики и не найдем лишних). Но при этом сплайн не жёстко привязан к спектру непрерывного рассеяния (в отличие от метода с поиском пиков) и может некорректно изогнуться в целях минимизации невязки. Поэтому метод коррекции энергетического дрейфа различными вариантами спуска по градиенту (в том числе и используемым в пакете Ньютоновским процессом) в этом случае работает хуже, чем в методе с поиском пиков - система становится слабо обусловленной. Неплохо работает глобальный поиск решения варьированием параметров дрейфа. Неопределённости оценивания при этом методе для хорошо разрешённых спектров не сильно отличаются от метода с поиском пиков - сказывается хорошая обусловленность системы уравнений. И поскольку решение задачи значительно ближе к линейному оцениванию, чем в методе с поиском пиков, неопределённости оцениваются корректнее.
Интерференция линийСпектры проб, содержащих уран и торий (пробы грунта, стройматериалов) или других нуклидов с большим количеством гамма линий, измеренные на спектрометре со сцинтилляционным гамма детектором, представляют собой один непрерывный мультиплет. Корректное разделение такого спектра на спектр пиков и спектр комптоновского рассеяния является непростой задачей. Не отделённый от спектра пиков спектр непрерывного комптоновского рассеяния делает все компоненты такого спектра накладывающимися друг на друга - интерферирующими. Поэтому необходимость разложения (декомпозиции) такого спектра на интерферирующие компоненты у большинства разработчиков программ обработки спектров сомнений не вызывает. Вот пример такого разложения (запись № 20 на странице "Гамма" журнала измерений демо версии пакета):
 Рис. 4. Декомпозиция сцинтилляционного гамма спектра.
В спектрах проб, измеренных на спектрометрах с охлаждаемыми полупроводниковыми детекторами, вследствие более чем на порядок лучшего разрешения, возможно корректное разделение спектра на спектр пиков и непрерывный спектр комптоновского рассеяния. По выделенным пикам можно судить о нуклидном составе спектра и, поставив в соответствие пикам линии нуклидов, оценить активность нуклидов. В программном пакете "СПЕКТР" это делает процедура предварительного анализа нуклидного состава. Большинство программ на этом и заканчивают обработку спектра, не решая проблему интерференции линий в пиках спектра (разделение мультиплетов на отдельные пики не решает задачу интерференции линий в таких разделённых пиках).
Может быть такая интерференция пренебрежимо мала или её нет совсем ?
Посмотрим, как выглядят спектры некоторых нуклидов измеренных на спектрометре с детектором из особо чистого германия:
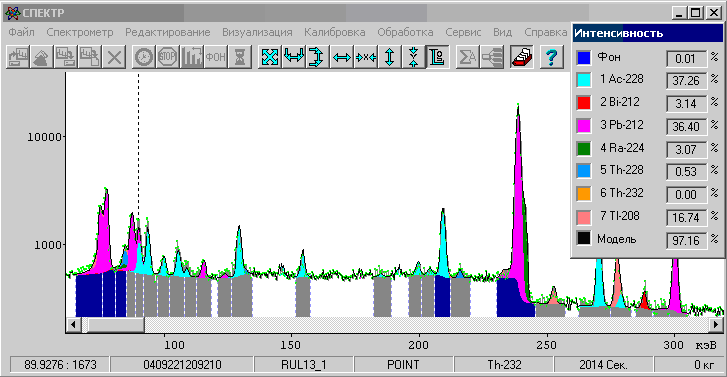 Рис. 5. Спектр 232Th с дочерними. Разрешение спектрометра для энергии 200 кэВ равно 1.67 кэВ
(запись 8 на странице "ППД спектрометрия" журнала измерений демо версии пакета) . .gif) Рис. 6. Спектр смеси эталонов, включающий нуклиды, часто применяемые для калибровки спектрометров
(запись 10 на странице "ППД спектрометрия" журнала измерений демо версии пакета) . На рисунках представлены результаты декомпозиции спектров, измеренных на гамма спектрометре с детектором из особо чистого германия.
Посмотрим на схемы гамма линий и гамма уровней при распаде нуклидов:  Рис. 7. Схема гамма уровней при распаде Bi-214 (дочернего нуклида в цепочке распада U-238). Данные сайта МАГАТЭ https://www-nds.iaea.org
 Рис. 8. Схема гамма уровней при распаде Ac-228 (дочернего нуклида в цепочке распада Th-232). Данные сайта МАГАТЭ https://www-nds.iaea.org
 Рис. 9. Таблица гамма линий цепочки распада природного урана в пакете "СПЕКТР".
В таблицу нуклидов. поставляемых с программным пакетом "СПЕКТР" включены, в основном, только сильные линии, тем не менее только цепочка распада природного урана при этом содержит 1868 линий. А при анализе любой пробы грунта надо учитывать ещё и цепочку Th-232.
Понятно, что даже в простых случаях чистые линии нуклидов найти сложно. Реальные пробы могут быть значительно сложнее. Кроме того, при решении экологических задач, программа должна разбираться со всеми пиками спектра в предположении, ну, если не нескольких тысяч гамма излучающих нуклидов существующих в природе, то сотни или двух нуклидов являющихся распространёнными продуктами деления или активации на фоне естественно радиоактивных, которые могут реально присутствовать в спектре пробы. Стандартная рабочая таблица нуклидов LongLive.ncl в пакете "СПЕКТР" содержит 10257 гамма линий принадлежащих 232 долгоживущим нуклидам. 232 нуклида объединены в 179 компонент декомпозиции (часть нуклидов объединена в равновесные цепочки).
В реальности даже решение задачи определения активности Ra-226, Th-232 и K-40 при определении А.эфф в пробах стройматериалов (обычная задача для организаций санэпиднадзора) без решения проблемы интерференции линий в пиках невозможно.
Например, определение активности калия (запись 15 на странице "ППД спектрометрия" журнала измерений демо версии пакета) .
 Рис. 10. Разложение спектра пробы грунта.
В данной пробе грунта калия мало, а тория много и в итоге вклад Ac-228 (дочки Th-232) в пик 1460.82 кэВ, используемый для оценки активности K-40, становится значимым. Корректное определение активности K-40 без учёта интерференции с Ac-228 невозможно.
Посмотрим на пик Ra-226 в пробе стройматериала (запись 29 на странице "ППД спектрометрия" журнала измерений демо версии пакета) :
 Рис. 11. Разложение пика 186 кэВ в спектре пробы стройматериалов.
Пик 186 кэВ является суперпозицией регистрации излучения 10 линий. Понятно, что без решения задачи интерференции линий оценка вклада линии Ra-226 невозможна.
Необходимость решения проблемы интерференции линий в пиках была очевидна для первых разработчиков программ обработки гамма спектров сразу после появление первых Ge(Li) детекторов в шестидесятых годах прошлого века (разрешение первых детекторов было не сильно хуже современных). Например, в статье R. Gunnink, J.B. Niday "Computerized quantitative analysis by gamma-ray spectrometry", vol.1 University of California, Lowrence Livermore Labaratory Report, UCRL-51061 (1972), авторы публикуют алгоритм формирования и решения системы уравнений по пикам спектра и линиям таблицы нуклидов. Подход был реализован в программе SAMPO, но развития не получил, поскольку SAMPO при сравнении программ показывала плохие результаты. Сами авторы объясняли это несовершенством алгоритма нелинейного МНК реализованного в программе. Надо добавить, что предложенный авторами подход к формированию системы уравнений из энергетических окон формируемых на основе найденных пиков, разрешения детектора и линий нуклидов, при большом количестве линий в таблице нуклидов приводит к формированию вырожденной системы уравнений. Задача в то время и не могла быть решена из-за слабых возможностей существовавших компьютеров.
В пакете "СПЕКТР" эта задача решена. Посмотрим, как это сделано в пакете «СПЕКТР»:
Формирование цепочек и смесей нуклидов
В математике существует единственный метод для повышения обусловленности системы уравнений (в общем, математической задачи) – включить в решение задачи дополнительную корректную информацию. В нашем случае, разумный и распространённый подход – дополнить нашу задачу информацией о связи активностей нуклидов:
Я упоминал, что это распространённый подход. В пакете «СПЕКТР» реализация этого метода сделана весьма удобной для использования – формирование равновесных цепочек и отдельных звеньев цепочек, формирование неравновесных цепочек и смесей нуклидов осуществляются несколькими нажатиями мышки.
Рассмотрим процесс формирования равновесных цепочек на примере создания таких цепочек из схемы распада U-238. Для этого потребуется вызвать программу создания и редактирования таблиц нуклидов (п. меню программы «СПЕКТР» «Сервис/Таблица нуклидов...»). В программе «Таблица нуклидов» выберем U-238 и посмотрим на его схему распада.
 Рис. 12. Дерево распада U-238.
Радиоактивное равновесие между U-238 и Ra-226 часто бывает нарушено. Поэтому в первую цепочку мы включим U-238, Th-234, Pa-234m, Pa-234, U-234 и Th-230. Для этого свернём схему распада ниже Th-230, щелкнув левой кнопкой мышки по значку слева от пиктограммы Th-230. В итоге схема примет вид:
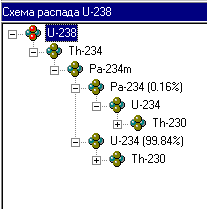 Процедура формирования цепочек не включает в цепочки нуклиды, не отображаемые в схеме распада. Поэтому, то, что мы свернули схему распада для Th-230, приведёт к тому, что в равновесную цепочку U-238 ,будут включены только Th-234, Pa-234m, Pa-234, U-234 и Th-230.
Запустим процедуру формирования равновесной цепочки из основного меню (п. меню «Сервис/Равновесная цепочка/Сформировать...») или вызвав всплывающее меню щелчком правой кнопки мышки по пиктограмме U-238. При этом программа попросит подтвердить серьёзность наших намерений.
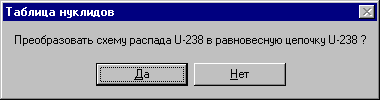 Ответ «Да» запускает процедуру формирования цепочки. В процессе формирования цепочки программа выясняет, что какие-то нуклиды или цепочки нуклидов входят в схемы распада других нуклидов и, в этом случае, формирует их копии. Нуклиды, входящие в копии цепочек, могут потребоваться для формирования других равновесных цепочек. При создании «копии цепочки» в действительности создаётся не копия нуклидов цепочки, а меняются атрибуты нуклидов таким образом, что нуклид приобретает статус «копия нуклида», вместо статуса «включён в равновесную цепочку». Это надо учитывать при желании самостоятельно удалить или отредактировать нуклид. Ответ «Да» запускает процедуру формирования цепочки. В процессе формирования цепочки программа выясняет, что какие-то нуклиды или цепочки нуклидов входят в схемы распада других нуклидов и, в этом случае, формирует их копии. Нуклиды, входящие в копии цепочек, могут потребоваться для формирования других равновесных цепочек. При создании «копии цепочки» в действительности создаётся не копия нуклидов цепочки, а меняются атрибуты нуклидов таким образом, что нуклид приобретает статус «копия нуклида», вместо статуса «включён в равновесную цепочку». Это надо учитывать при желании самостоятельно удалить или отредактировать нуклид.По завершению анализа и создании копий цепочек нуклидов, программа выводит на экран окно расчёта активности нуклидов выбранной части схемы распада на текущую дату с начальной датой, соответствующей требованию необходимой продолжительности распада для формирования равновесного состояния цепочки:
 Рис. 13. Форма процедуры расчёта активности цепочки нуклидов.
В соответствии со значениями последней колонки таблицы «Доля в активности материнского %» рассчитываются квантовые выходы для линий нуклидов, включённых в равновесную цепочку. Можно отметить, что активность U-234 и Th-230 в нашем примере несколько выше 100% (доли в распаде) - это происходит всегда по истечении некоторого времени требуемого для формирования равновесности в цепочке за счёт некоторого преобладания процесса накопления дочерних нуклидов в цепочке над процессом распада. Абсолютной равновесности не бывает. В случае если период полураспада материнского нуклида в цепочке более чем в десять раз больше периода полураспада самого долгоживущего из дочерних нуклидов, считается что требование необходимое для формирования радиоактивного равновесия в цепочке выполняется. В этом случае редактирование данных в форме расчёта активности запрещено, и форма имеет только информативный характер. В противном случае программа сообщит, что радиоактивное равновесие в цепочке никогда не наступит и, разрешив редактирование данных в форме расчёта активности, предложит оператору самому задать требуемое состояние соотношения активностей нуклидов в цепочке.
Нажав на клавишу «Ввод», в итоге получим следующую схему распада для U-238:
 Все линии Th-234, Pa-234m, Pa-234, U-234 и Th-230 включены в соответствии с квантовых выходом и долей в активности материнского U-238. Цепочка Rn-222 - Po-214 также может быть объединена в равновесную. Для этого мы переключимся в таблице изотопов на Rn-222 и свернём схему распада ниже Po-214 и Tl-210. Получим следующую схему распада: Все линии Th-234, Pa-234m, Pa-234, U-234 и Th-230 включены в соответствии с квантовых выходом и долей в активности материнского U-238. Цепочка Rn-222 - Po-214 также может быть объединена в равновесную. Для этого мы переключимся в таблице изотопов на Rn-222 и свернём схему распада ниже Po-214 и Tl-210. Получим следующую схему распада: . Вызвав процедуру формирования равновесной цепочки для Rn-222, получим в итоге схему распада U-238, включающего две равновесные цепочки U-238-Th-230 и Rn-222 -Po-214 и итоговую таблицу линий для U-238 включающую линии дочерних: . Вызвав процедуру формирования равновесной цепочки для Rn-222, получим в итоге схему распада U-238, включающего две равновесные цепочки U-238-Th-230 и Rn-222 -Po-214 и итоговую таблицу линий для U-238 включающую линии дочерних:  Рис. 14. Сформированная равновесная цепочка U-238.
Сформированная равновесная цепочка легко преобразуется обратно в набор отдельных нуклидов вызовом пункта меню «Сервис/ Равновесная цепочка/ Расформировать...».
Использование полной функции спектра компоненты
Оконный метод при решении задачи декомпозиции – подход традиционный до недавнего времени. При оконном методе итоговая система уравнений формируется из квантовых выходов линий нуклидов и интегральных окон спектра пробы соответствующим пикам спектра и линиям нуклидов. Её достоинство – малая чувствительность к энергетическому дрейфу спектрометра. При широком окне дрейф внутри окна никак не сказывается на результате. Недостаток – пренебрежение информацией о форме линии, а потеря информации влечёт ухудшение обусловленности системы и уменьшение эффективности оценок. Ухудшение обусловленности нередко бывает катастрофическим – при рабочей таблице нуклидов включающей сотню или две нуклидов итоговые системы уравнений становятся вырожденными.
Альтернативный метод – использование полной функции спектров компонент. В этом методе спектр пробы не приводится к интегральным окнам. Соответственно квантовый выход линии должен быть преобразован в функцию отклика спектрометра. Гамма линия имеет определённую энергию и нулевую ширину (дельта функция). При регистрации она расплывается в пик определённой ширины (спектр комптоновского рассеяния предварительно вычитается). Форма пика близка к гауссиану, но в реальности, естественно, не гауссиан. Её можно описать сколь угодно точно самыми различными комбинациями элементарных функций. Но для нас крайне важно, чтобы число свободных параметров определяющих форму линии было минимальным, поскольку обусловленность системы быстро уменьшается с ростом числа свободных параметров (конструкция становится шаткой).
В пакете «СПЕКТР» реализовано два подхода к построению модели линии:
Гауссиан используется в том случае, если оператор не выполнил процедуру расчёта моделей линий по спектру эталона. В случае если результаты обработки спектра при использовании гауссиана нас удовлетворяют (реальные модели линий весьма схожи с гауссианом), можно и не проводить расчёт моделей линий.
Расчёт моделей линий производится с учётом интерференции линий (программа не требует, чтобы пик спектра формировался только одной гамма линией). Преимущество второго подхода в том что, в качестве модели линии мы получим реальный отклик спектрометра и при большом числе каналов спектрометра достаточно хорошо описывающий его форму при минимальном числе свободных параметров (положение и ширина линии). Недостаток – функция хранится в виде таблицы и для вычисления производных функции (часто требуемая операция) приходится прибегать к процедуре численного дифференцирования, что вносит некоторые дополнительные погрешности.
В пакете «СПЕКТР» реализованы оба подхода к обработке спектров и оконный и альтернативный. Выбор того или иного метода производится установкой или снятием галочки в форме параметров шаблона обработки.
 Рис. 15. Форма установки параметров шаблона обработки спектров.
Поскольку оконный метод может приводить к вырожденности системы уравнений (при вырожденности системы отсутствует единственное решение), процедура решения в случае вырожденности будет спрашивать у оператора, какой из двух нуклидов делающих решение неоднозначным следует исключить из системы. Режим работы в этом случае получается диалоговым, а не автоматическим. Чтобы этого не происходило, оператор имеет возможность поделить все нуклиды рабочей таблицы на 10 сортов, присвоив каждому нуклиду определённый ранг. В этом случае, программа обратится к оператору только в том случае, если придётся делать выбор между нуклидами одного ранга.
Альтернативный метод – метод разложения спектра на спектры компонент предъявляет более жёсткие требования и к спектрометру и компьютеру спектрометра. Поскольку, в этом случае, энергетический дрейф спектрометра может существенно исказить результаты обработки, в модель в качестве дополнительных неизвестных параметров включаются и параметры описывающие энергетический дрейф спектрометра. Система уравнений становится нелинейной. Решение больших нелинейных систем требует хорошей производительности компьютера. К счастью развитие компьютерной техники позволяет сейчас решать задачи, о которых вчера и не мечтали.
Включение в систему уравнений в качестве неизвестных параметров энергетического дрейфа спектрометра, дрейфа разрешения и Z эффективное пробы приводит к следующей модели спектра:
Здесь:
Множитель
Z- отклонение условного Z эффективное пробы от Z эффективное пробы соответствующего химическому составу вещества счётного образца.
E(i)- энергия канала i.
Scomp(i) – спектр непрерывного рассеяния (комптоновское рассеяние гамма квантов и тормозное рентгеновское бета частиц) для спектра пробы. Рассчитывается процедурой поиска пиков при предварительной обработке спектра.
Pn(i)- сплайн. Сплайн используется при разложениии гамма спектра для аппроксимации спектра непрерывного рассеяния, в том случае если спектр непрерывного рассеяния не определён процедурой предварительной обработки спектра (Scomp(i)=0).
i- канал спектра.
Свёртка с функцией рассеяния
В общем случае предполагаются независимые значения параметров дрейфа для всех компонент. Если все компоненты разложения находятся в единой энергетической шкале, оператор может указать в табличке параметров декомпозиции, что спектры компонент находятся в единой шкале, то есть
Оператор может исключить из списка параметров
Методика оценки активностей и расчёта погрешностей при такой модели спектра подробно изложена в статье «Проблемы и решения в сцинтилляционной гамма спектрометрии ». Отличие процедуры оценки активностей только в том, что в ППД гамма спектрометрии модель дополнительно содержит спектр комптоновского рассеяния. Ковариационную матрицу спектра комптоновского рассеяния также полагаем диагональной
Расчёт погрешностей отличается от сцинтилляционной модели тем, что в ППД методике присутствует процедура поиска пиков имеющая нелинейный характер. Дисперсия оценок средних за время измерения активностей в этом случае вычисляется следующим образом:
Посмотрим на обработку реального спектра в разных режимах (запись 2 на странице "ППД спектрометрия" журнала измерений демо версии пакета) .
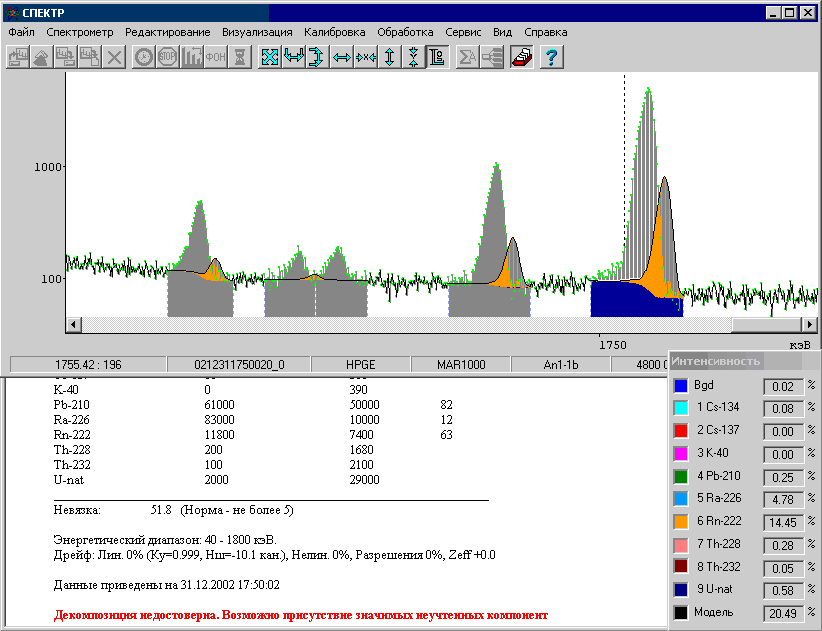 Рис. 16. Результаты обработки без коррекции дрейфа.
На рисунке представлены результаты обработки спектра подсыпки под полом загрязнённой Ra-226 (спектр измерен в Московском городском центре санэпиднадзора 31.12.2002 года). Показан высокоэнергетический хвост спектра, поскольку именно там лучше проявляются эффекты, связанные с энергетическим дрейфом. Достаточно большая активность Ra-226 приводит к существенному энергетическому дрейфу спектрометра. На рисунке представлены результаты обработки без коррекции дрейфа. Результаты никуда не годные (невязка разложения = 51.8).
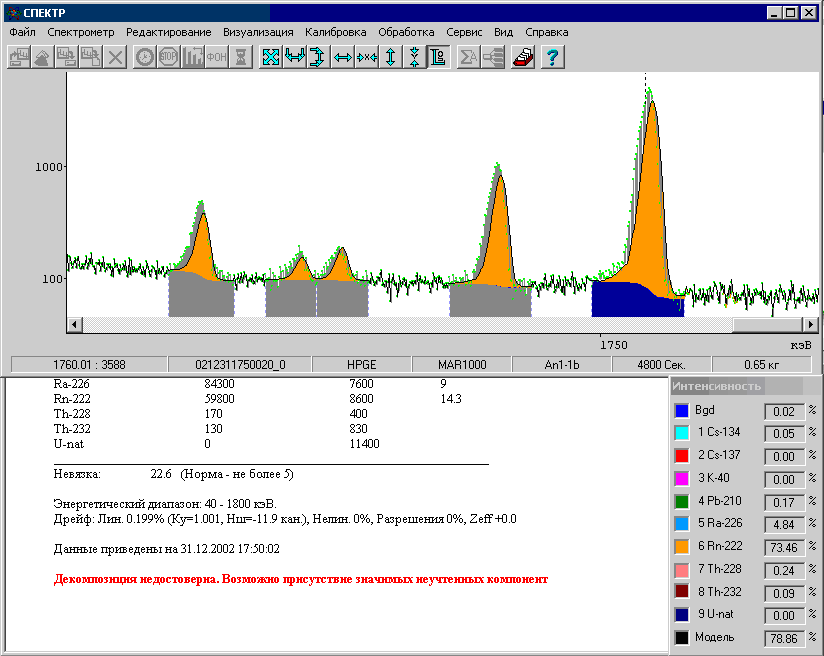 Рис. 17. Результаты обработки с коррекцией линейного дрейфа.
На рисунке представлены результаты обработки того же спектра, но с коррекцией линейного дрейфа (параметры a и b в модель спектра включены). Результаты значительно лучше (невязка = 22.6), но от идеала очень далеки.
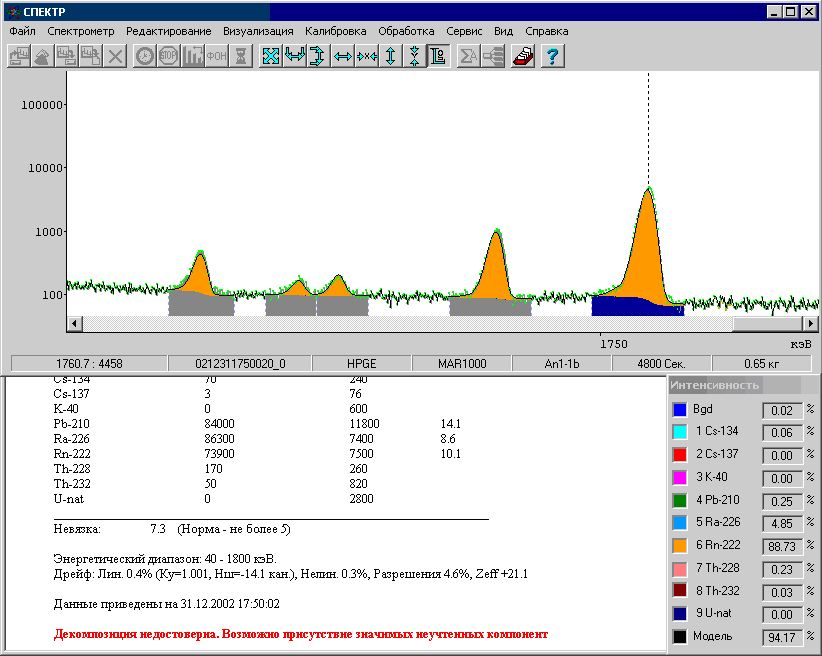 Рис. 18. Результаты обработки с коррекцией нелинейного дрейфа, разрешения и Z эффективное.
На рисунке окончательный вариант обработки, включающий и разрешение на варьирование Z эффективное. Значительное улучшение невязки (невязка = 7.3). Существенно изменилась оценка активности Pb-210. Она стала ближе к активности Ra-226, что очень похоже на правду, поскольку проба является подсыпкой из под пола (что-то, чем было засыпано межэтажное перекрытие под деревянным полом) квартиры на шестом этаже старого дома - не химически агрессивная среда и радиоактивное равновесие между Ra-226 и Pb-210 весьма вероятно.
Невязка разложения выше нормы, но добиться малой невязки при приличной статистике и активной пробе на данном спектрометре практически невозможно, поскольку начинают сказываться эффекты, не учитываемые в нашей модели спектра. Старенький Рижский детектор времён начала перестройки и старенькая электроника фирмы «Аспект» не выдерживает загрузки – пики расплываются в основаниях, а наша модель пика такую хитрую деформацию формы пика не предполагает. В данном случае, поскольку число компонент разложения невелико, лучше работает оконный метод (естественно, после коррекции энергетического дрейфа).
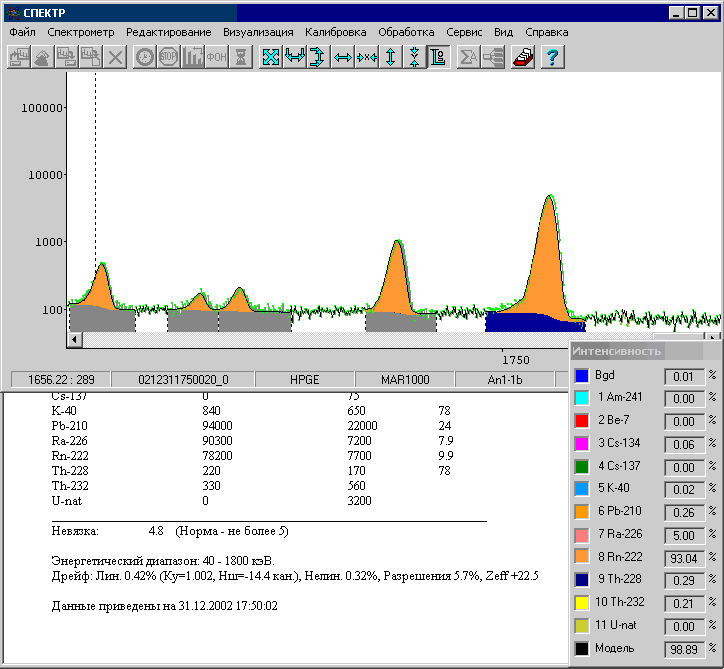 Рис. 19. Результаты обработки оконным методом с коррекцией нелинейного дрейфа, разрешения и Z эффективное.
Обработка оконным методом после коррекции энергетического дрейфа даёт значительно меньшую невязку разложения, поскольку нюансы, связанные с формой пика, уже не учитываются.
Поглощение излучения в веществе пробыПри прохождении через вещество гамма кванты взаимодействуют с электронами и ядрами атомов вещества. При взаимодействии они либо поглощаются в результате фотоэлектрического эффекта, либо теряют часть своей энергии и изменяют направление в результате комптоновского рассеяния и эффекта рождения электрон – позитронных пар (есть ещё ряд эффектов, но наиболее существенны три указанных). При малых энергиях гамма квантов, наиболее значимым является фотоэффект. При энергиях квантов Eγ ≥1022 кэВ, возникает эффект рождения электрон-позитронных пар. Совместное действие эффектов характеризуется полным линейным коэффициентом ослабления гамма квантов в веществе
Где n -концентрация атомов вещества в единице объема, σ -полное эффективное сечение взаимодействия.
Здесь ρ - плотность среды , Na - число Авогадро , A -молярная масса атомов среды.
В энергетическом диапазоне от 30 кэВ до 3000 кэВ
Z – заряд ядер атомов вещества счётного образца, Eγ- энергия гамма излучения.
 Рис. 20. Сечение реакций взаимодействия гамма квантов с глиной (Z = 7.6).
На рисунке представлены сечения трёх основных реакций взаимодействия гамма квантов с веществом (кв.см/г) для счётного образца почвы (глины). Для энергий более 100 кэВ сечение фотопоглощения на порядок меньше сечения комптоновского рассеяния, сечение эффекта образования пар в диапазоне до 4000 кэВ также более чем на порядок слабее комптоновского рассеяния. Практически для основной массы исследуемых в Санэпиднадзоре веществ (продукты питания, почва и т.п.) единственным значимым эффектом является комптоновское рассеяние. Но встречаются пробы и с большими значениями Z:
 Рис. 21. Сечение реакций взаимодействия гамма квантов с вольфрамом (Z = 74).
На рисунке показаны аналогичные сечения реакций для образца вольфрама (в Московском центре гигиены и эпидемиологии пришлось исследовать образцы электродов из торированного вольфрам - запись № 12 на странице "ППД спектрометрия" журнала измерений демо версии пакета ). В этом случае влияние фотоэффекта превышает влияние комптоновского рассеяния до энергии 470 кэВ.
Взаимодействие гамма излучения с веществом на пути от возникновения гамма кванта до регистрации в детекторе отражается в функциях эффективности регистрации гамма квантов определяемых при калибровке спектрометра. Но в комплексе счётный образец – детектор есть непостоянная часть – сам счётный образец. Поглощение излучения при прохождении через стенки измерительного сосуда, упаковку детектора и сам детектор при неизменной геометрии измерений остаётся постоянным, меняется поглощение излучения в веществе счётного образца. Это поглощение зависит от плотности, химического состава и толщины счётного образца.
Число гамма квантов на выходе из счётного образца, которые пролетят без взаимодействия с веществом пробы, выражается формулой:
N0– число гамма квантов для вакуума, x – эффективная толщина счётного образца.
В пакете «СПЕКТР» используются четыре функции эффективности регистрации:
Наиболее зависимой от процессов взаимодействия гамма квантов с веществом пробы является функция эффективности регистрации гамма квантов в фотопиках. Например:
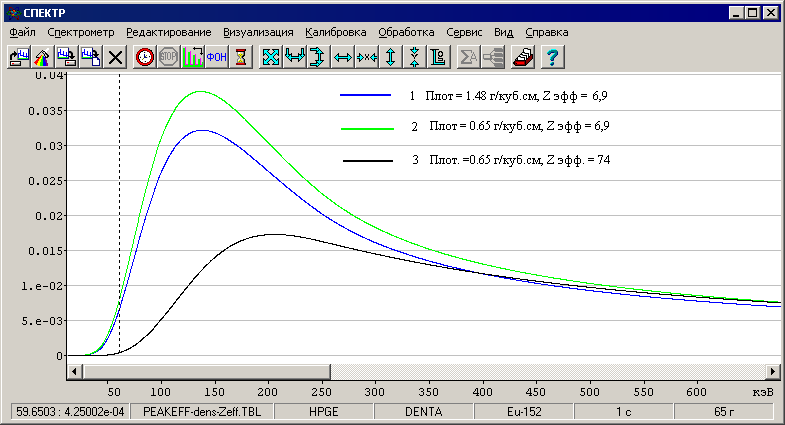 Рис. 22. Функции эффективности регистрации в фотопиках.
На рисунке представлены три функции эффективности регистрации в фотопиках:
Счётным образцом были кусочки электродов из торированного вольфрама. Кроме продуктов из радиоактивной цепочки распада 232Th в пробе, естественно ничего не было, но если бы там был, например, 241Am и оператор не предпринял бы ничего, чтобы учесть большое Z эффективное пробы, оценка активности 241Am была бы занижена в ~40 раз.
Функция полной эффективности регистрации гамма квантов в спектрометре необходима для корректного учёта процессов регистрации каскадных гамма квантов. Она зависит практически только от процессов фотопоглощения. Комптоновское рассеяние помешает зарегистрироваться гамма кванту в фотопике, но общее число зарегистрированных гамма квантов в спектрометре практически не меняется. Эффект образования пар увеличивает число гамма квантов, но вероятность регистрации не меняется, поскольку процесс происходит в очень малый промежуток времени, один, два или все три гамма кванта зарегистрируются в спектрометре как один импульс.
Функции эффективности регистрации в пиках утечки требуются для корректной оценки гамма квантов регистрируемых в пиках утечки и аннигиляционном пике. Основной вклад в формирование пиков утечки вносит эффект формирования пар непосредственно в материале детектора, а не в веществе пробы. Это происходит вследствие того что эффект образования пар приводит к появлению трёх гамма квантов вместо одного и их регистрация в пиках утечки происходит уже по законам совпадений, так же как для каскадных переходов. Вероятность регистрации двух или трёх гамма квантов на порядок больше, если эти гамма кванты родились непосредственно в детекторе, а не далеко от детектора в пробе (эффективность регистрации уменьшается как квадрат расстояния от детектора). Для того чтобы рассчитать процесс формирования пар по формулам, без использования эталонов, требуется знание конструкции детектора и материалов конструкции детектора, что далеко не всегда известно. Проще и надежнее, на мой взгляд, провести калибровку эффективности регистрации гамма квантов в пиках утечки. Для этого требуется эталон, содержащий нуклиды, имеющие гамма линии с энергией более 1500 кэВ, например, 232Th в радиоактивном равновесии с дочерними нуклидами. Для приемлемой калибровки эффективности регистрации в пиках утечки для энергетического диапазона до 3000 кэВ достаточно и одной точки, поскольку вторая (начальная) точка известна, а зависимость эффективности регистрации в пиках утечки от энергии в нашем энергетическом диапазоне достаточно точно аппроксимируется выражением ln(E).
В пакете «СПЕКТР» процессы, происходящие в счётном образце, учитываются и при перерасчёте функций эффективности регистрации в пиках утечки, но в реальности вклад их очень мал.
Для корректного перерасчёта функций эффективности регистрации в соответствии с параметрами счётного образца требуется знание плотности пробы, эффективной толщины пробы и химического состава вещества счётного образца. Оценка плотности при измерениях в фиксированной геометрии проблем не вызывает – достаточно взвесить счётный образец, сложнее с химическим составом пробы. Нередко оператор не знает химического состава пробы. В этом случае программа предполагает что всё вещество счётного образца состоит из одного элемента имеющего заряд ядер равный условному Z эффективное и массу ядер равную условной эффективной атомной массе.
В пакете «СПЕКТР» предусмотрено несколько вариантов решения проблемы:
Задание химического состава вещества счётного образца оператором
База данных по химическим формулам вещества счётного образца в пакете «СПЕКТР» объединена с базой данных по нормативам (СанПиН, НРБ и т.п.). Оператор при запуске измерений должен выбрать из списка или создать тип пробы с требуемыми значениями физических констант. Форма процедуры создания – редактирования данных по физическим константам и нормативам выглядит следующим образом:
 Рис. 23. Форма создания и редактирования констант и нормативов.
Оператор может ввести формулу вещества пробы для трёх вариантов счётных образцов. Отсутствие формулы означает, что эти данные оператору неизвестны. В этом случае программа может попытаться определить требуемые данные непосредственно по измеренному спектру
Определение поглощения излучения по спектру пробы
В том случае если спектр пробы содержит нуклиды, имеющие гамма линии и в мягкой и в жёсткой области спектра, можно рассчитать поглощение излучения непосредственно по спектру пробы, поскольку зависимость поглощения гамма излучения от энергии известна. Точность оценки будет тем выше, чем больше разница в активности нуклида, рассчитанная по мягким и жёстким линиям. Для включения процедуры расчёта поглощения излучения по спектру пробы в процесс обработки спектра достаточно установить галочку «Варьирование Z эффективное пробы» в параметрах шаблона обработки. Поглощение излучения в веществе счётного образца зависит и от толщины счётного образца. Для непростых геометрий затруднительно точно определить эффективную толщину счётного образца, поэтому рекомендуется включить и варьирование толщины пробы. Это замедлит обработку, но позволит получить более точные оценки активностей нуклидов.
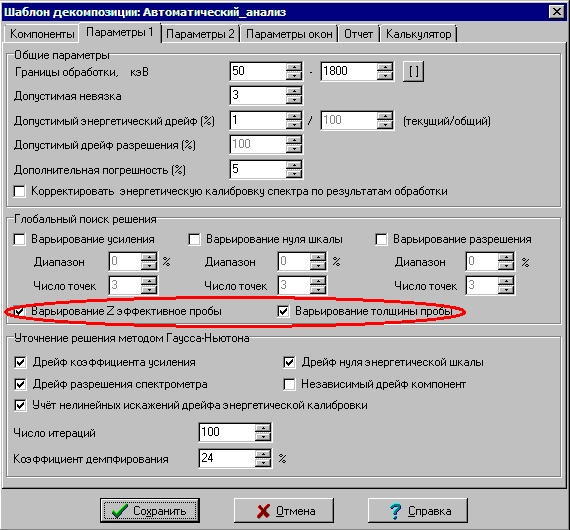 Рис. 24. Форма создания и редактирования параметров шаблонов декомпозиции.
В нашем примере с обработкой спектра пробы из торированного вольфрама Z эффективное определяется равным 73.3, что вполне соответствует истине:
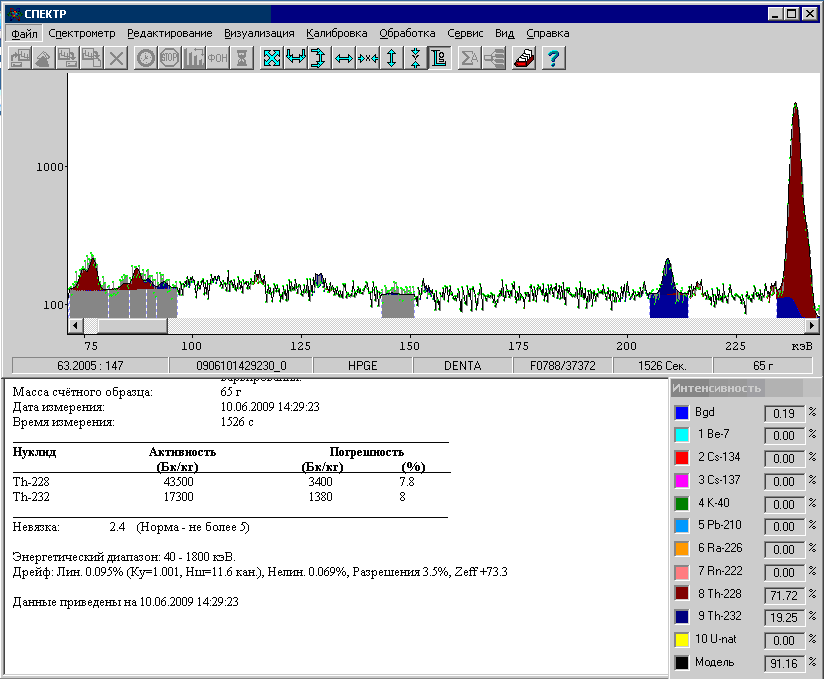 Рис. 25. Результаты обработки спектра с варьированием Z эффективное.
Сравните результаты с обработкой того же спектра, но без варьирования Z эффективное (на следующем рисунке).
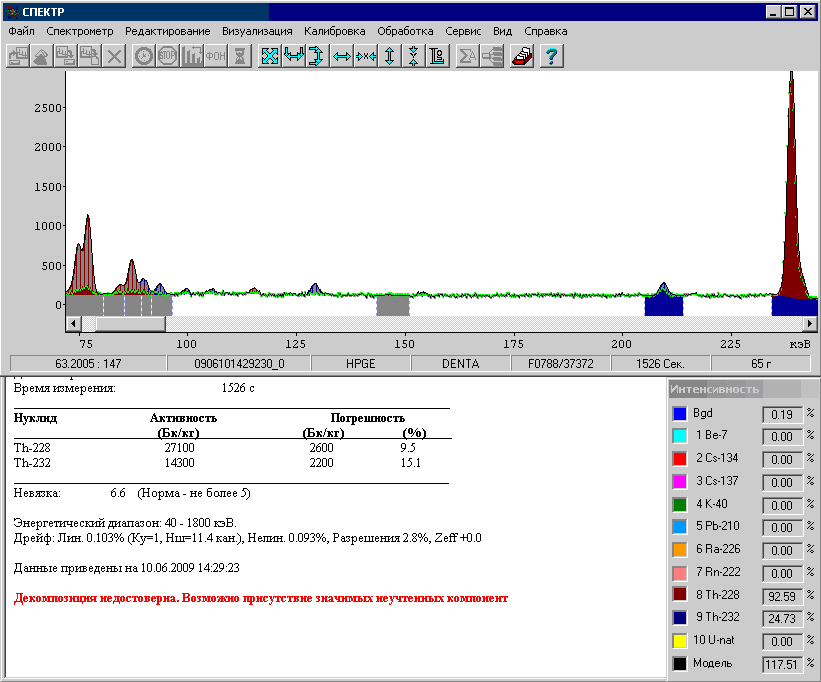 Рис. 26. Результаты обработки спектра без варьирования Z эффективное.
На рисунке видно, что в мягкой области спектра большая невязка (спектр Th-228 значительно выше спектра пробы) вследствие того, что не было учтен эффект фотопоглощения при большом Z эффективное пробы.
Определение поглощения излучения по спектру пробы и априорной информации
В случае если проба не содержит нуклидов, имеющих линии и в мягкой (менее 100 кэВ), где значим процесс фотопоглощения, и в жёсткой (более 500 кэВ) области энергий, где он влияет слабо, автоматическое определение Z эффективное не работает, поскольку итоговая система уравнений становится вырожденной. В этом случае процедура решения системы уравнений исключает Z эффективное и эффективную толщину пробы из списка неизвестных. Для того чтобы и в данном случае итоговая система уравнений не была вырожденной, можно дополнить её априорной информацией об активностях нуклидов имеющих линии в мягкой области энергий. Для этого потребуется либо химическое выделение требуемого нуклида и оценка его активности другими методами, либо добавление в счётный образец нуклида известной активности отсутствующего в пробе. В пакете «СПЕКТР» предусмотрена процедура учёта априорной информации об активностях нуклидов пробы либо вводимая оператором вручную, либо из файлов результатов обработки или архива измерений. Процедура решения итоговой системы уравнений использует помехоустойчивый вариант Байесовского оценивания.
Пики утечки Гамма кванты с энергией более 1022 кэВ, при взаимодействие с веществом, могут образовывать электрон-позитронные пары. 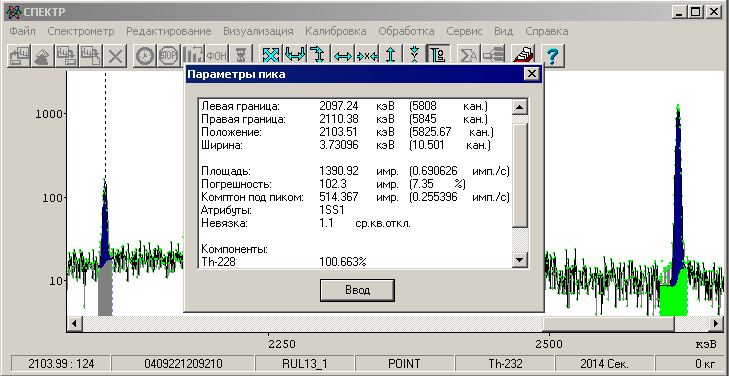
Рис. 27. Пик одиночной утечки (2103.5 кэВ) в спектре Th-232.
На рисунке пик одиночной утечки от линии Th-232 с энергией 2614.5 кэВ. Площадь пика составляет 10.2 % от основного.
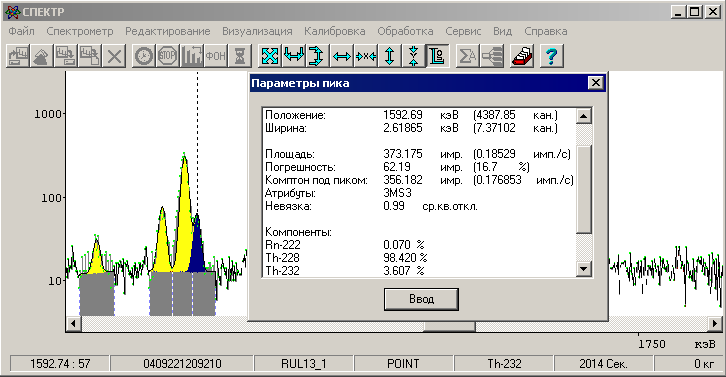 Рис. 28. Пик двойной утечки (1592.5 кэВ) в спектре Th-232.
На рисунке пик двойной утечки от линии Th-232 с энергией 2614.5 кэВ. Площадь пика составляет 2.74 % от основного
Вероятность регистрации образовавшихся трёх гамма квантов в том или другом пике зависит от эффективности регистрации гамма квантов фотопиках и полной эффективности регистрации в детекторе. Такие пары образуются и в счётном образце и в материалах детектора, но большую вероятность зарегистрироваться одновременно имеют гамма кванты, образовавшиеся непосредственно в детекторе. Для расчёта данного эффекта по формулам требуется знание и конструкции и материалов детектора, что далеко не всегда известно.
В пакете «СПЕКТР» для учёта эффектов образующих пики утечки используется калибровка функций эффективности регистрации гамма квантов в пиках одиночной и двойной утечки.
 Рис. 29. Таблицы эффективности регистрации используемые в пакете "СПЕКТР".
Эффекты образования пар, происходящие в счётном образце, учитываются при перерасчёте функций эффективности регистрации в пиках утечки, но в реальности вклад их очень мал.
Каскадные гамма квантыДля детекторов с хорошей эффективностью регистрации становятся существенны проблемы, связанные с регистрацией каскадных гамма квантов. Каскадные гамма кванты – кванты, родившиеся в процессе одной реакции распада с промежутком времени в единицы, десятки и сотни пикосекунд (до единиц наносекунд). Такие гамма кванты в современных спектрометрах, если регистрируются, регистрируются как один импульс. А каскадную схему распада имеют очень многие нуклиды.
Посмотрим на примере расчёта функции эффективности регистрации в фотопиках для эталона на основе Eu-152 измеренного на хорошем детекторе (HPGe, паспортная эфф. рег =120%) как сказывается учёт или не учёт особенностей регистрации каскадных гамма квантов.
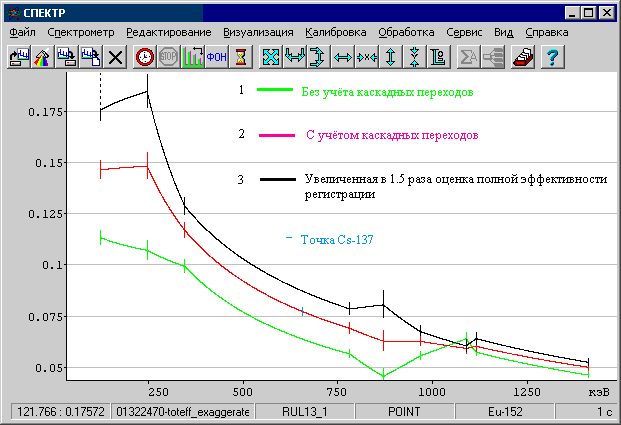 Рис. 30. Эффективность регистрации гамма квантов в фотопиках.
«Эффективность регистрации в фотопиках - это отношение числа зарегистрированных в пике определённой энергии импульсов к числу излучённых гамма квантов данной энергии». К сожалению, это определение годится только для одиночных гамма квантов, а не гамма квантов летящих каскадом (на нашем рисунке такому условию отвечает точка, полученная при измерении Cs-137).
Для каскадных гамма квантов вероятность регистрации кванта в фотопике:
В итоге, если не учитывать указанные поправки мы получим эффективность регистрации, показанную на графике 1 (рассчитанные точки кривой эффективности отображаются вертикальными линиями и для наглядности соединены отрезками экспонент). В данном случае большой коаксиальный HPGe детектор n-p типа имеет максимум эффективности регистрации в области 150 кэВ (правее левой точки – 122 кэВ), а все точки от второй должны бы попасть с той или иной точностью на экспоненту. Это не происходит – есть существенные выбросы и в целом эффективность регистрации сильно занижена (для точки Cs-137, 661 кэВ, на ~ 15%).
Точность поправок зависит от точности калибровки полной эффективности регистрации. Третий график иллюстрирует, что произойдёт, если полная эффективность регистрации окажется завышенной.
Что требуется для учёта эффектов связанных с каскадной схемой распада:
В настоящее время пакет «СПЕКТР» поставляется с библиотекой включающей 526 наиболее распространённых нестабильных нуклидов. В библиотеку включена информация о каскадной схеме распада для сильных гамма линий всех нуклидов. Библиотека постоянно обновляется. Последнее обновление соответствует данным ENSDF от января 2019 года скачанным с сайта МАГАТЭ https://www-nds.iaea.org/relnsd/vcharthtml/VChartHTML.html
Информация о каскадных переходах является частью информации о гамма линии. Соответственно, процедура редактирования информации о каскадных схемах распада в пакете «СПЕКТР» - это процедура редактирования параметров гамма линии. Форма процедуры выглядит следующим образом (на примере редактирования одной из линий Co-60):
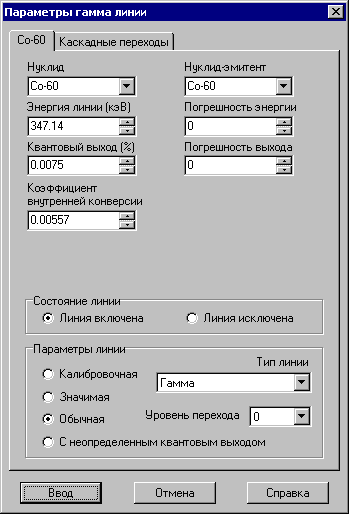 Рис. 31. Форма редактирования параметров гамма линии.
Вторая страница формы - «Каскадные переходы»:
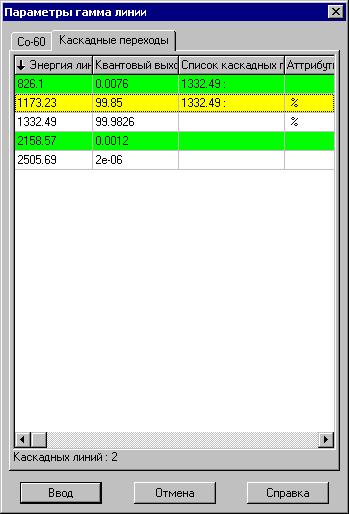 Рис. 32. Информация о каскадных переходах для линии Co-60 с энергией 347.14 кэВ.
Таблица содержит список всех линий нуклида за исключением редактируемой. Линии, формирующие непосредственный каскад с редактируемой линией, выделяются зелёным или синим цветом. Оператор может включить линию в список каскадных или исключить из него двойным щелчком по линии или с помощью всплывающего меню.
Требуется помечать как каскадные только линии, формирующие непосредственный каскад с редактируемой. Например, в схеме распада Co-60:
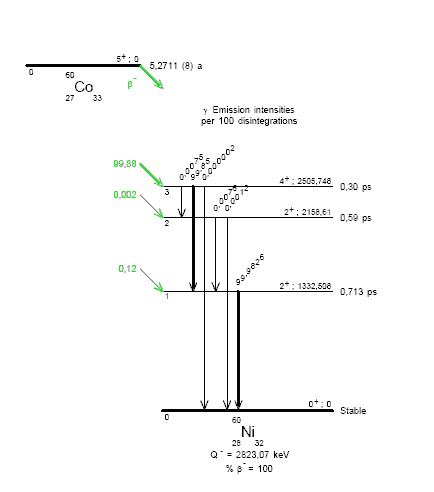 Рис. 33. Схема распада Co-60 в Ni-60.
Для линии, формируемым переходом с 3-его уровня на 2-ой (Q=0.0075), требуется указать как каскадные линии, образуемые переходом нуклида с 2-ого уровня на первый (Q=0.0076) и со второго на нулевой (Q=0.0012) - предыдущий рисунок.
Для линии, формируемым переходом с 3-его уровня на 1-ый (Q=99.85), требуется указать как каскадную линию, образуемую переходом нуклида с 1-ого уровня на нулевой (Q=99.9826) – следующий рисунок.
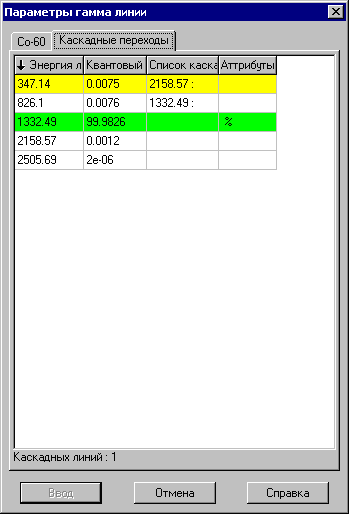 Рис. 34. Информация о каскадных переходах для линии Co-60 с энергией 1173.23 кэВ.
Подключение информации о каскадной схеме распада к процедуре обработки спектра осуществляется вызовом пункта меню «Сервис/ Линии сложения каскадных/ Включить в таблицу» и установки отредактированной таблицы нуклидов в качестве рабочей в параметрах шаблона обработки.
 Рис. 35. Подключение таблицы нуклидов в шаблон обработки.
Для расчёта вероятности регистрации каскадного гамма кванта в фотопике, спектре комптоновского рассеяния или в пике сложения каскадных требуется, кроме информации о линии (энергия, выход, коэффициент внутренней конверсии и информация о каскадных), функции эффективности регистрации гамма квантов в фотопиках и полной эффективности регистрации в спектрометре.
Для калибровки полной эффективности регистрации рекомендуется использовать нуклиды имеющие либо только одну линию (таких нуклидов я не помню), либо с одной наиболее мощной линией (Am-241, Cd-109, Co-57, Ce-139, Sn-113, Cs-137, Mn-54, Zn-65, Co-60, K-40). Процедура калибровки эффективности в пакете «СПЕКТР» рассчитывает полную эффективность регистрации для любого эталона с любым числом линий (при этом рассчитывается усреднённая энергия и усреднённый выход), но вопрос о подключении рассчитанной точки в таблицу полной эффективности регистрации оставляет на усмотрение оператора. Практика показала, что использование даже одной точки в таблице полной эффективности регистрации (например, рассчитанной для Eu-152) существенно улучшает ситуацию с расчётом каскадных эффектов, чем при отсутствии такой точки (итоговая полная эффективность регистрации для заданной энергии в процедуре обработки использует информацию и об эффективности регистрации в фотопиках). Но если мы имеем несколько точек для различных энергий полной эффективности регистрации рассчитанных по монолиниям, включение точки рассчитанной усреднением по ряду линий вряд ли улучшит итоговую таблицу полной эффективности регистрации.
Рентгеновская флуоресценцияГамма излучение от пробы вызывает рентгеновскую флуоресценцию вещества пробы, конструкционных материалов защиты и детектора. Чем интенсивней излучение, тем интенсивнее флуоресценция. Если в пробе или в конструкционных материалах присутствуют материалы с большим Z (зарядом ядра атомов), то наведённое рентгеновское излучение может попасть в энергетический диапазон, используемый при обработке гамма спектра и его, в этом случае, требуется учитывать. Что произошло, например, при исследовании пробы электродов из торированного вольфрама (запись № 12 на странице "ППД спектрометрия" журнала измерений демо версии пакета) в лаборатории санэпиднадзора г. Москвы: Рис. 36. Обработка без учёта рентгеновской флуоресценции.
Обработка без учёта рентгеновской флуоресценции - компоненты рентгеновской флуоресценции интерпретированы как Am-241, но декомпозиция недостоверна, поскольку форма компонент рентгеновской флуоресценции существенно отличается от формы Am-241.
 Рис. 37. Обработка с учётом рентгеновской флуоресценции. Корректное определение активности Am-241.
В пакете "СПЕКТР" для учёта рентгеновской флуоресценции необходимо установить соответствующую галочку в параметрах используемого шаблона обработки:
 Рис. 38. Подключение процедуры включения компонентов рентгеновской флуоресценции в шаблон обработки.
Боюсь, что немалое число "специалистов" в области спектрометрии не представляют и не приемлют никакого другого способа определение активностей, кроме как метода оценки активностей по площади пика в предположении, что пик формируется единственной линией. Пакет "СПЕКТРРАД" вполне удовлетворит и таких любителей времени логарифмических линеек и арифмометров. Достаточно в шаблоне декомпозиции снять все галочки и установить одну - "Оконный метод обработки". Затем капитально покромсать используемую библиотеку нуклидов, оставив из десятка тысяч линий только сильные линии (не больше сотни). Процедура обработки будет работать так как это принято, скажем, в пакете "GammaVision" или "Genie-2000", Ругаться, к сожалению, будет на недостоверность результатов. Но и это можно исправить - достаточно в шаблоне обработки установить галочку "Использовать только значимые линии для расчёта невязок".
Но, надо подчеркнуть, что только решение задачи декомпозиции измеренного спектра с учётом всех перечисленных выше эффектов и расчёте итоговой невязки декомпозиции позволяет проводить качественный и надёжный анализ нуклидного состава пробы.
25 апреля 2013 г. Обновлён 14.12.2023 г.
Дрёмин Геннадий Иванович. |