Сцинтилляционная гамма спектрометрияДо недавнего времени в гамма спектрометрии существовало два основных типа детекторов: сцинтилляционные детекторы, преобразующие энергию гамма кванта в световой импульс (наиболее распространённый вариант детектора - на основе кристалла NaI(Tl)), и ППД детекторы (HPGe - особо чистый германий, Ge(Li), Si(Li)) на основе твердотельных полупроводниковых кристаллов. ППД детекторы требовали для работы охлаждения до температуры жидкого азота. Разрешение сцинтилляторов NaI(Tl) зависит от объёма, но для наиболее распространённых детекторов редко было меньше 7 % по линии 662 кэВ. Разрешение ППД детекторов по той же линии могло быть и меньше 0.3 %. В последнее время появилось много новых детекторов и в классе сцинтилляторов (SrI2, LaBr и другие) и ППД детекторы, не требующие охлаждения (CZT). Для обработки спектров важно только разрешение. Разрешение детектора либо позволяет успешно отделить спектр пиков от спектра непрерывного рассеяния (комптоновского рассеяния гамма квантов и тормозного рентгеновского бета частиц), либо не позволяет, либо такая операция работает плохо. Поэтому в моей терминологии под сцинтилляционной гамма спектрометрией имеется ввиду гамма спектрометрия с детекторами, не обеспечивающими высокого разрешения гамма линий и обработка таких спектров без отделения спектра пиков от спектра непрерывного рассеяния. Рассмотрим основные проблемы, которые приходится решать при обработке сцинтилляционных гамма спектров и методы их решения, реализованные в программном пакете «СПЕКТР»: Энергетическое разрешение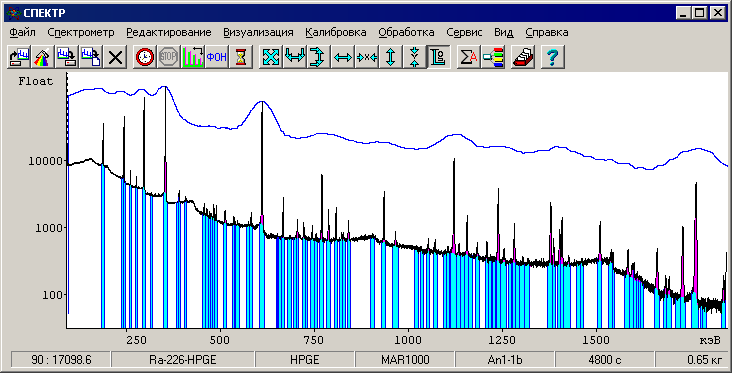 Рис. 1. Спектр Ra-226 с продуктами распада.
Во времена царя Гороха, когда считать приходилось пользуясь логарифмическими линейками и арифмометрами, активность нуклидов в пробах измеренных на ППД спектрометрах определялась по отношению площадей отдельных пиков в спектре пробы и спектре эталона. В сцинтилляционной спектрометрии выделить отдельный пик вследствие плохого энергетического разрешения спектрометра можно только в редких искусственных случаях. Если в пробе присутствуют цепочки естественно радиоактивных урана и тория, то сцинтилляционный гамма спектр такой пробы будет представлять один сплошной мультиплет от 0 до 3 МэВ. На рис. 1 представлен спектр Ra-226 с дочерними продуктами распада в относительно равновесном состоянии измеренный на детекторе из особо чистого германия (нижний спектр) и спектр той же пробы измеренный на сцинтилляционном детекторе NaI(Tl) (верхний спектр). Разрешение ППД спектрометра - 2 кэВ по линии 1332 кэВ, разрешение сцинтиллятора - 8% по линии 661 кэВ – средние значения для большинства аналогичных детекторов.
 Рис. 2. Цепочка распада природного урана.
Спектры проб содержащих естественно радиоактивные нуклиды, кроме U-nat (32 нуклида в цепочке распада, около 2000 заметных линий) содержат ещё не менее богатую пиками цепочку распада Th-232 (12 нуклидов в цепочке распада и более 350 значимых гамма линий, не считая линий сложения каскадных и линий утечки).
 Рис. 3. Спектр пиков (без комптона) природного урана измеренного на сцинтилляционном спектрометре с 8 % разрешением по линии 662 кэВ.
Невозможность для большинства сцинтилляционных спектров выделения каких-либо пиков (не говоря уже о «чистых» пиках отдельных нуклидов) заставляла решать систему уравнений сформированных из интегральных энергетических окон, включающих и спектр непрерывного рассеяния. Каналы спектра являются такими энергетическими окнами. Невысокая скорость расчётов на логарифмической линейке ограничивала количество окон и заставляла объединять каналы спектра в более крупные энергетические окна. Но при этом нарушается требование теоремы Гаусса-Маркова, выпонение которого необходимо для получения наиболее эффективных оценок и малое количество окон не позволяет корректно оценить норму вектора отклонения модели от объекта, позволяющую судить о достоверности оценок активности нуклидов. Поэтому, при наличии компьютера, такое интегрирование спектра является совершенно не нужной операцией.
Рассмотрим коротко основные методы обработки сцинтилляционных гамма спектров:
1. Разложение спектра на компоненты включающие и спектр непрерывного рассеяния.
 Рис. 4. Разложение спектра пробы содержащей Cs-137 и K-40 на компоненты включающие и спектр непрерывного рассеяния (запись 0 на странице "Поверка" журнала измерений демоверсии пакета).
 Рис. 5. Разложение спектра пробы содержащей ЕРН на компоненты включающие и спектр непрерывного рассеяния (запись 18 на странице "Гамма" журнала измерений демоверсии пакета).
Метод позволяет получить наиболее эффективные оценки активностей (в качестве неопределённостей приведены случайные составляющие неопределённостей), оценить и скорректировать энергетический дрейф спектрометра, корректно оценить достоверность оценок. Основным недостатком метода является сложность калибровки спектрометра использующего такой метод обработки спектров. Обычный вариант расчёта полных откликов спектрометра на излучение нуклидов (компонентов разложения) - расчёт из измеренных спектров эталонов. При этом для каждой используемой геометрии требуются и эталоны в той же геометрии (перерасчёт с одной геометрии на другую геометрию невозможен). И если мы собираемся измерять активность сотни нуклидов, то и эталонов потребуется как минимум 101 (плюс один эталон фоновой пробы). А для учёта поглощения в зависимости от плотности - как минимум 201 эталон. Метод расчёта поглощения по сечениям реакций прекрасно работает только для ППД метода обработки - оценкой активности нуклидов по пикам спектра.
2. Поиск пиков и разложение спектра на спектры пиков нуклидов.
 Рис. 6. Разложение спектра пиков пробы содержащей Cs-137 и K-40 на спектры пиков нуклидов (запись 0 на странице "Поверка" журнала измерений демоверсии пакета).
До последнего времени - основной метод обработки ППД спектров. Метод замечательно работает и для сцинтилляционных спектров, если нуклидов и гамма линий в спектре немного и разрешение детектора позволяет корректно разделить спектр пробы на спектр пиков и спектр непрерывного рассеяния. Метод замечателен тем, что спектры пиков нуклидов легко рассчитываются по таблицам нуклидов и калибровкам спектрометра. Без проблем рассчитывается поглощение гамма квантов в зависимости от плотности и химического состава пробы.
В случае сложного нуклидного состава пробы результаты намного хуже:  Рис. 7. Поиск пиков и разложение спектра пиков для пробы содержащей ЕРН на спектры пиков нуклидов (запись 18 на странице "Гамма" журнала измерений демоверсии пакета).
Вследствие невозможности корректно отделить спектр пиков от спектра непрерывного рассеяния, оценки активностей нуклидов занижены (торий, практически, потерялся). И поскольку контроль достоверности оценивания по норме вектора отклонения модели от объекта корректно работает только для класса линейных оценок, оценка достоверности декомпозиции не верна (нюансы связанные с неверным разделением спектра на спектр пиков и спектр непрерывного рассеяния учитываются плохо). Надо заметить, что и при линейном оценивании норма вектора равна сумме квадратов координат только в ортогональном базисе (сумма квадратов катетов равна квадрату гипотенузы только при ортогональносьти катетов). А для неортогонального надо учитывать метрический тензор пространства. В данном случае использование для оценки достоверности критерия согласия Пирсона, строго подходя, некорректно.
Для современных сцинтилляционных детекторов с разрешением менее 3% по линии 662 кэВ расширяется круг задач при которых возможно корректное выделение спектра пиков. Но при этом учёт интерференции линий в пиках обязателен - чем хуже разрешение, тем чаще интерференция. И если даже для ППД спектров учёт интерференции необходим, то тем более он нужен для сцинтилляционных.
3. Разложение спектра на спектры пиков нуклидов и аппроксимация спектра непрерывного рассеяния.
 Рис. 8. Разложение спектра для пробы содержащей ЕРН на спектры пиков нуклидов с аппроксимацией спектра непрерывного рассеяния полиномом.
Спектр непрерывного рассеяния имеет очень сложную форму и удовлетворительная аппроксимация его полиномом во всей области обработки невозможна (полином хорошо работает только на коротких отрезках), что и демонстрирует рис. 8. Оценки линейные и поэтому контроль достоверности работает корректно (об этом и говорит красный цвет записей по нуклидам - процедура оценки достоверности корректно оценивает оценки активностей как недостоверные). В целом оценки и активностей и неопределённостей для данного спектра корректнее, чем при обработке с поиском пиков (рис. 7).
 Рис. 9. Разложение спектра для пробы содержащей ЕРН на спектры пиков нуклидов с аппроксимацией спектра непрерывного рассеяния сплайном (запись 18 на странице "Гамма" журнала измерений демоверсии пакета, шаблон обработки "ЕРН+Cs-137_SPLINE, ранг сплайна равен 3).
Использование сплайна вместо полинома существенно улучшает оценки. Невязка декомпозиции снизилась до приемлего уровня. Но поскольку мы добавили в слабо обусловленную задачу ещё несколько десятков неизвестных (коэффициентов сплайна), неопределённость оценивания существенно выросла. В данном шаблоне обработки ранг сплайна был задан равным 3 (кубический сплайн). Посмотрим, что получится при использовании кусочно линйной аппроксимации. В этом случае мы в два раза сократим число неизвестных определяющих сплайн:
 Рис. 10. Разложение спектра для пробы содержащей ЕРН на спектры пиков нуклидов с аппроксимацией спектра непрерывного рассеяния сплайном (запись 18 на странице "Гамма" журнала измерений демоверсии пакета, шаблон обработки "ЕРН+Cs-137_SPLINE, ранг сплайна равен 1).
Использование кусочно-линейной аппроксимации спектра непрерывного рассеяния позволило существенно снизить оценки неопределённостей при сохранении невязки оценивания.
 Рис. 11. Разложение спектра пробы содержащей Cs-137 и K-40 на спектры пиков нуклидов с аппроксимацией спектра непрерывного рассеяния сплайном (запись 0 на странице "Поверка" журнала измерений демоверсии пакета).
Метод разложения спектров с использованием сплайна позволяет смешивать в списке компонентов декомпозиции компоненты представляющие собой полный отклик спектрометра на излучение нуклида (включающий и спектр непрерывного рассеяния) и компоненты являющиеся спектрами пиков для нуклида (без спектра непрерывного рассеяния). В итоге мы повышаем эффективность оценивания.
 Рис. 11-1. Разложение спектра пробы содержащей Cs-137 и K-40 на полный спектр K-40 и спектр пиков Cs-137 с аппроксимацией комптона от Cs-137 сплайном.
Метод незаменим при обработке сложных сцинтилляционных спектров, если полные отклики спектрометра (включающие и спектр непрерывного рассеяния) некоторых нуклидов мы не можем рассчитать по спектрам эталонов либо из-за их малого времени жизни (Pb-212, Bi-212, например, при анализе аэрозолей в воздухе), либо трудностей с изготовлением таких эталонов (большая бочка, геометрия 2π или 4π), либо при большом числе нуклидов в исследуемой пробе (оценка концентрации остаточного U-235 в отработанном ядерном топливе, оценка активностей нуклидов в РАО). В возможности MCNP метода я верю слабо.
Намного проще рассчитать спектры пиков по калибровкам эффективности регистрации, моделям пиков и таблицам нуклидов. При этом легко рассчитывается и поглощение гамма квантов во всех трёх средах (материал счётного образца, контейнер и среда между источником и детектором). Корректно осуществляется расчёт для объёмной эффективности регистрации по точечной геометрии, корректно учитываются проблемы каскадных переходов и линий утечки. Энергетический дрейфИ если в ППД спектрометрии процедура оценки активности нуклида по площади пика устойчива к энергетическому дрейфу спектрометра (мы можем ошибиться с идентификацией пика, но площадь его останется неизменной при любом дрейфе спектрометра), оконный метод в сцинтилляционной спектрометрии весьма чувствителен к энергетическому дрейфу спектрометра. А сцинтилляционные тракты, к сожалению, дрейфуют – то есть коэффициент преобразования сцинтилляционных детекторов не стабилен, а изменяется с течением времени. Дрейф зависит от времени работы тракта, температуры, интенсивности регистрируемого излучения и стабильности питания.
Всевозможные схемы стабилизации работают плохо. Почему? Да потому что невозможно без качественной полной обработки спектра решить задачу стабилизации. Сплошь и рядом в схемах стабилизации используется обратная связь (коэффициент усиления упал – поднимем коэффициент усиления и наоборот). Но любая обратная связь с инерционными элементами (а безинерционных элементов в природе не существует) приводит к осцилляциям, а значит, разрешение портится. А нет никакой нужды использовать обратную связь, когда у нас под рукой компьютер – можно просто пересчитывать спектр, либо добавлять при регистрации импульса не единичку в один канал, а, например, 0.8 в один канал, и 0.2 в соседний, в соответствии со значениями параметров дрейфа.
Но этого мало. Схемы стабилизации, как правило (точнее всегда) корректируют только один параметр – коэффициент усиления, а такая схема не годится. Практика показывает, что требуется корректировать как минимум три параметра: дрейф коэффициента усиления, дрейф нуля, а поскольку дрейф, связанный с загрузкой спектрометра и не нулевым внутренним сопротивлением источников питания, по идее, нелинейный, то и коэффициент нелинейных искажений. При попытке использовать для коррекции только один пик, три параметра мы никак определить не можем. Мы и один то параметр определяем очень плохо. Почему? Предположим, мы используем светодиод генерирующий импульсы определённой амплитуды закреплённый у ФЭУ. В этом случае мы можем, конечно, генерировать импульсы любой интенсивности и проблема малой статистики снимается, но остаются проблемы стабильности импульсов от светодиода, проблема коррекции мёртвого времени и проблема только одного реперного пика. Если мы используем реперный источник – он портит спектр, да и наложение измеряемого спектра на репер искажает стабилизацию. Предположим мы используем пики самой пробы или фоновый калий-40. Но при этом различный нуклидный состав пробы может как угодно смещать стабилизацию, поскольку излучение других нуклидов (в том числе и K-40 – его положение в спектре отличается от положения фонового K-40) накладывается на фоновый K-40. Не поможет и стабилизация по пику 2614.5 кэВ Tl-208, поскольку пики сложения каскадных линий от нуклидов цепочки распада Ra-226 накладываются и на этот пик. Замечательно работает только одна схема стабилизации – полная обработка всего спектра, включающая в качестве определяемых параметров и параметры энергетического дрейфа. Эффективных оценок (в том числе и оценок параметров дрейфа) можно добиться, только используя всю корректную информацию об объекте корректно. Посмотрим на результаты обработки «сдрейфовавшего» спектра (запись № 17 на странице "Гамма" журнала измерений демо версии пакета):
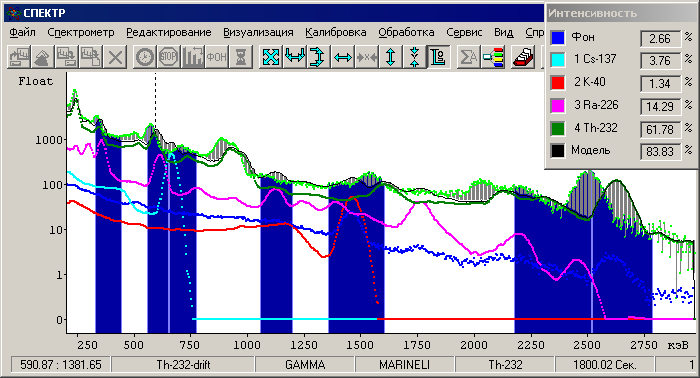 Рис. 12. Обработка спектра оконным методом без коррекции дрейфа.
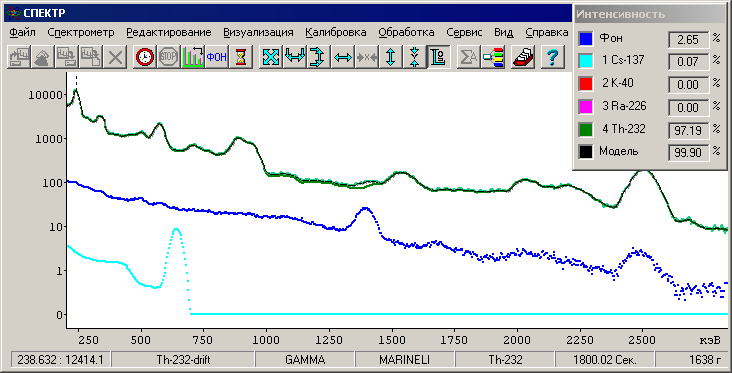 Рис. 13. Обработка спектра стандартным методом с коррекцией дрейфа.
Табл. 1. Результаты обработки На рис. 12 представлена итоговая картинка разложения спектра пробы (в качестве пробы эталон Th-232) оконным методом (7 интегральных окон), на рис. 13 – картинка разложения спектра стандартным для пакета «Спектр» методом и в таблице 1 – результаты обработки тем и другим методом.
Из сравнения ясно, что даже небольшой (вполне обычный для сцинтилляционных спектрометров) 5-процентный энергетический дрейф приводит при решении системы методом без коррекции энергетического дрейфа к катастрофическим результатам. Дрейф спектрометра может быть связан с активностью пробы и, в этом случае, не компенсируется предварительной процедурой энергетической калибровки.
Процедура решения линейной системы в пакете «Спектр» корректно оценивает погрешности решения и поэтому, хотя результаты решения задачи «оконным методом» никуда не годятся (слишком большие неопределённости оценок активностей), математически они вполне корректны (истинные значения лежат в пределах доверительного интервала) и поэтому не приведут к неверному заключению. Не все программы настолько корректны в оценке погрешностей и в данном случае вполне могли бы выдать, например, результат по Cs-137 110 ± 20 – а такой результат ошибочен и может привести к неверным выводам.
Очевидно, что, энергетический дрейф спектрометра надо учитывать и при оценке активностей и при оценке погрешностей, поскольку при любых схемах стабилизации тракта мы не можем быть уверены в отсутствии энергетического дрейфа.
Метод и модель
«Стандартным» для пакета «Спектр» методом разложения спектра на компоненты является разложение спектра помехоустойчивым Байесовским методом с коррекцией энергетического дрейфа и дрейфа разрешения спектрометра. Надо отметить, что метод также является оконным, только энергетических окон много (обычно чуть меньше, чем каналов спектра). Большое количество окон позволяет включить в модель в качестве неизвестных параметры энергетического дрейфа и параметры поглощения излучения в веществе счётного образца.
Модель спектра при этом выглядит следующим образом:
Здесь:
.gif) – спектры компонент (нормированные на число распадов спектры излучения отдельных нуклидов или цепочек нуклидов, находящихся в состоянии радиоактивного равновесия). – спектры компонент (нормированные на число распадов спектры излучения отдельных нуклидов или цепочек нуклидов, находящихся в состоянии радиоактивного равновесия)..gif) – амплитуды соответствующих компонент. – амплитуды соответствующих компонент..gif) , , .gif) и и .gif) – параметры энергетического дрейфа спектрометра. – параметры энергетического дрейфа спектрометра. Множитель
Z- отклонение условного Z эффективное пробы от Z эффективное пробы соответствующего химическому составу вещества счётного образца.
E(i)- энергия канала i.
Pn(i)- сплайн (сплайн используется при разложениии гамма спектра на спектры пиков для аппроксимации спектра непрерывного рассеяния).
i- канал спектра.
Свёртка с функцией рассеяния
В общем случае предполагаются независимые значения параметров дрейфа для всех компонент. Если все компоненты разложения находятся в единой энергетической шкале, оператор может указать в табличке параметров декомпозиции, что спектры компонент находятся в единой шкале, то есть
Оператор может исключить из списка параметров
Решение
Используем метод Гаусса – Ньютона. Начальное значение вектора параметров находим, используя глобальное варьирование выбранных параметров в заданном диапазоне с заданным шагом. Быстродействие современных компьютеров, пока что не позволяет варьировать все параметры с достаточной плотностью сетки, поэтому оператор может задать в параметрах декомпозиции варьирование пяти основных параметров: Z эффективное пробы, толщины пробы, коэффициента усиления, нуля шкалы и разрешения спектрометра. Найденное приближение уточняем, используя ньютоновский процесс.
Здесь:
Средняя за время измерения активность k – ого нуклида:
 Здесь:
El, Er - левая и правая энергетические границы декомпозиции, e - энергия;
Значения активностей на момент начала измерений для одиночных нуклидов, нуклидов равновесных цепочек и материнских нуклидов цепочек распада:
Здесь:
Для нуклидов входящих в цепочку распада решение не описывается выражением из элементарных функций, а является численным решением системы интегральных уравнений:
 Здесь:
Оценка погрешностей
Мы предполагаем, что спектр
Здесь:
Значения в каналах спектра фона полагаем коррелированными (если фон увеличился, то он увеличился, вероятно, во всех каналах).
Здесь:
В итоге:
Здесь:
и
То есть мы используем оценки погрешностей линеаризованной модели дополненной погрешностями, связанными с обрывом итерационного процесса (погрешности дрейфа спектрометра).
Дисперсии оценок средних за время измерения активностей:
Здесь:
Дисперсии оценок активностей на момент начала измерений для одиночных нуклидов, нуклидов равновесных цепочек и материнских нуклидов цепочек распада:
Здесь:
Дисперсии для нуклидов входящих в цепочку распада рассчитываются при решении системы интегральных уравнений описывающих распад и накопление нуклидов в процессе измерения:
 Решением является линейное преобразование
Итоговая полная погрешность i - ой активности:
Оценка погрешности соответствует 95% доверительному интервалу.
Двадцать пять лет использования такого подхода к обработке сцинтилляционных спектров в десятках организаций Москвы и Московской области доказали его высокую эффективность и надёжность.
Поглощение излучения в веществе пробыПри прохождении через вещество гамма кванты взаимодействуют с электронами и ядрами атомов вещества. При взаимодействии они либо поглощаются в результате фотоэлектрического эффекта, либо теряют часть своей энергии и изменяют направление в результате комптоновского рассеяния и эффекта рождения электрон – позитронных пар (есть ещё ряд эффектов, но наиболее существенны три указанных). При малых энергиях гамма квантов (до сотен кэВ), наиболее значимым является фотоэффект. При энергиях квантов Eγ ≥1022 кэВ, возникает эффект рождения электрон-позитронных пар. Влияние комптоновского рассеяния преобладает в промежуточной энергетической области. Совместное действие эффектов характеризуется полным линейным коэффициентом ослабления гамма квантов в веществе
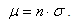 Где n -концентрация атомов вещества в единице объема, σ -полное эффективное сечение взаимодействия.
Здесь ρ - плотность среды , Na - число Авогадро , A -молярная масса атомов среды.
.gif) - сечения фотоэффекта, комптоновского рассеяния и эффекта образования пар. - сечения фотоэффекта, комптоновского рассеяния и эффекта образования пар.В энергетическом диапазоне от 30 кэВ до 3000 кэВ
Z – заряд ядер атомов вещества счётного образца, Eγ- энергия гамма излучения.
 Рис. 14. Сечение реакций взаимодействия гамма квантов с глиной (Z = 7.6).
На рис. 14 представлены cечения трёх основных реакций взаимодействия гамма квантов с веществом (кв.см/г) для счётного образца почвы (глины). Для энергий более 100 кэВ сечение фотопоглощения на порядок меньше сечения комптоновского рассеяния, сечение эффекта образования пар в диапазоне до 4000 кэВ также более чем на порядок слабее комптоновского рассеяния. Практически для основной массы исследуемых в Санэпиднадзоре веществ (продукты питания, почва и т.п.) единственным значимым эффектом является комптоновское рассеяние. Но встречаются пробы и с большими значениями Z:
 Рис. 15. Сечение реакций взаимодействия гамма квантов с вольфрамом (Z = 74).
На рис. 15 показаны аналогичные сечения реакций для образца вольфрама (в Московском центре гигиены и эпидемиологии пришлось исследовать образцы электродов из торированного вольфрама). В этом случае влияние фотоэффекта превышает влияние комптоновского рассеяния до энергии 470 кэВ.
Число гамма квантов на выходе из счётного образца, которые пролетят без взаимодействия с веществом пробы, выражается формулой:
N0– число гамма квантов для вакуума, x – эффективная толщина счётного образца.
Формула (1) вполне годится для расчёта поглощения гамма квантов в веществе счётного образца для метода обработки спектров связанных с выделением пиков (ППД спектрометрия), поскольку при любом взаимодействии гамма кванта с веществом этот гамма квант уже не зарегистрируется в пике полного поглощения – он будет потерян для обработки связанной с разложением спектра пиков (небольшое исключение составляет эффект образования пар, но этот эффект играет роль не в счётном образце, а в самом детекторе).
В сцинтилляционной спектрометрии (при обработке без выделения пиков) формула (1) в общем случае не работает – гамма кванты, испытавшие комптоновское рассеяние, могут не зарегистрироваться в детекторе, а могут и зарегистрироваться в спектре комптоновского рассеяния. Рассчитать, где в спектре зарегистрируется гамма квант (если зарегистрируется) после комптоновского рассеяния, очень непросто. В последнее время появилось много работ использующих для такого расчёта процедуру, основанную на разработанном в Los Alamos National Laboratory методе MСNP (Monte Carlo N-Particles transport code). К сожалению трудности связанные с корректным учётом комптоновского рассеяния гамма квантов, тормозного рентгеновского бета частиц остаются и при использовании этого метода – для учёта всех эффектов связанных с рассеянием квантов требуется детальное описание не только системы счётный образец – детектор, но и защиты вокруг образца с детектором. Пока что мне не встречались работы убедительно доказывающие, что точность расчётов эффектов связанных с рассеянием гамма и рентгеновских квантов с использование данного метода меньше, скажем, 10 %. Поэтому естественным выходом является перерасчёт (интерполяция или экстраполяция) спектров компонент на заданную плотность (комптоновское рассеяние пропорционально плотности электронов, а плотность электронов пропорциональна плотности счётного образца) по спектрам компонент, рассчитанным из эталонов различной плотности, приведённых к заданному эффективному заряду атомов и эффективной атомной массе. А перерасчёт на заданный эффективный заряд и эффективную атомную массу, то есть учёт фотопоглощения производить по формуле поглощения излучения в веществе (1). Именно такая процедура и реализована в программном пакете «Спектр».
Оценка плотности при измерениях в фиксированной геометрии проблем не вызывает – достаточно взвесить счётный образец, сложнее с химическим составом пробы. Нередко оператор не знает химического состава пробы. В этом случае программа предполагает что всё вещество счётного образца состоит из одного элемента имеющего заряд ядер равный условному Z эффективное и массу ядер равную условной эффективной атомной массе.
В пакете «СПЕКТР» предусмотрено несколько вариантов решения проблемы:
Задание химического состава вещества счётного образца оператором
База данных по химическому составу вещества счётного образца в пакете «СПЕКТР» объединена с базой данных по нормативам (СанПиН, НРБ и т.п.). Оператор при запуске измерений должен выбрать из списка или создать тип пробы с требуемыми значениями химического состава. Форма процедуры создания – редактирования данных по физическим константам и нормативам выглядит следующим образом:
 Рис. 16. Форма создания и редактирования констант и нормативов.
Оператор может ввести формулу вещества пробы для трёх вариантов счётных образцов. Отсутствие формулы означает, что эти данные оператору неизвестны. В этом случае программа может попытаться определить требуемые данные непосредственно по измеренному спектру
Определение поглощения излучения по спектру пробы
В том случае если спектр пробы содержит нуклиды, имеющие гамма линии и в мягкой и в жёсткой области спектра, можно рассчитать поглощение излучения непосредственно по спектру пробы, поскольку зависимость поглощения гамма излучения от энергии известна. Точность оценки будет тем выше, чем больше разница в активности нуклида, рассчитанная по мягким и жёстким линиям. Для включения процедуры расчёта Z эффективное по спектру пробы в процесс обработки спектра достаточно установить галочку «Варьирование Z эффективное пробы» в параметрах шаблона обработки. Поглощение излучения в веществе счётного образца зависит и от толщины счётного образца. Для непростых геометрий затруднительно точно определить эффективную толщину счётного образца, поэтому рекомендуется включить и варьирование толщины пробы. Это замедлит обработку, но позволит получить более точные оценки активностей нуклидов.
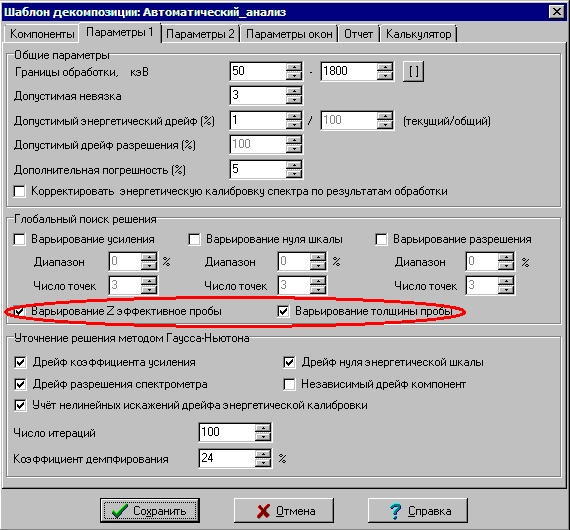 Рис. 17. Форма создания и редактирования параметров шаблонов декомпозиции.
На следующих двух рисунках представлены результаты обработки спектра электродов из торированного вольфрама измеренные на сцинтилляционном детекторе в Московском центре гигиены и эпидемиологии. Торий искусственного происхождения находится, как правило, в неравновесном состоянии, поэтому спектр раскладывается на две цепочки тория: Th-232 – Ac-228 и Th-228 – Tl-208.
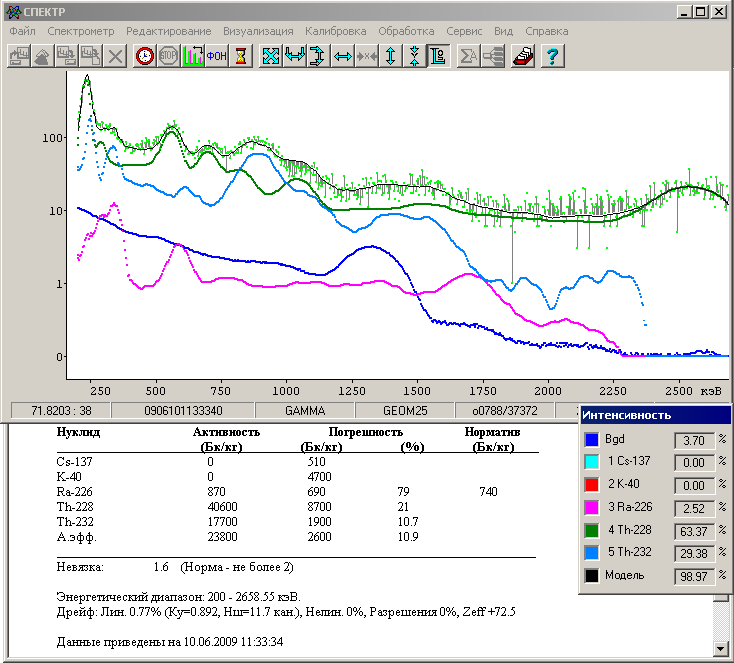 Рис. 18. Результаты обработки спектра с варьированием Z эффективное.
Сравните результаты с обработкой того же спектра, но без варьирования Z эффективное (на следующем рисунке).
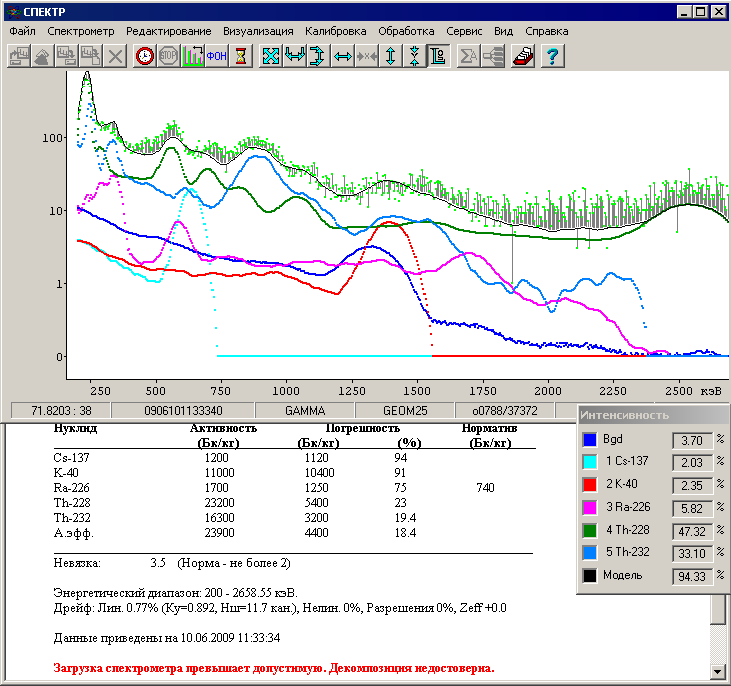 Рис. 19. Результаты обработки спектра без учёта Z эффективное.
Значения активности Th-228 при обработке спектра без учёта Z эффективное существенно занижено, вследствие того, что не было учтен эффект фотопоглощения при большом Z эффективное пробы.
Определение поглощения излучения по спектру пробы и априорной информации
В случае если проба не содержит нуклидов, имеющих линии и в мягкой (менее 100 кэВ), где значим процесс фотопоглощения, и в жёсткой (более 500 кэВ) области энергий, где он влияет слабо, автоматическое определение Z эффективное не работает, поскольку итоговая система уравнений становится вырожденной. В этом случае процедура решения системы уравнений исключает Z эффективное и эффективную толщину пробы из списка неизвестных. Для того чтобы и в данном случае итоговая система уравнений не была вырожденной, можно дополнить её априорной информацией об активностях нуклидов имеющих линии в мягкой области энергий. Для этого потребуется либо химическое выделение требуемого нуклида и оценка его активности другими методами, либо добавление в счётный образец нуклида известной активности отсутствующего в пробе. В пакете «СПЕКТР» предусмотрена процедура учёта априорной информации об активностях нуклидов пробы либо вводимая оператором вручную, либо из файлов результатов обработки или архива измерений. Процедура решения итоговой системы уравнений использует помехоустойчивый вариант Байесовского оценивания.
8 октября 2011 г. Обновлён 14.12.2023 г.
Дрёмин Геннадий Иванович. |
||||||||||||||||||||||

.gif)